LeetCode - 1. Two Sum

문제 개요

난이도 - EASY 사용 언어 - C++

입력값은 정수형 배열 nums와 정수형 target이 제공됩니다. nums에서 두 숫자를 더해 target과 동일한 값이 나오는 배열 인덱스 두 개를 반환하면 됩니다.

문제 - LeetCode - 1. Two Sum

예시

입력 : nums = [2,7,11,15] target = 9

출력 : [0,1]

제약조건

배열 내 같은 숫자는 재사용할 수 없다.
답은 정확히 하나만 존재한다.

풀이

Solution 1 - Brute force

첫 번째로 떠올린 방법은 Brute force 즉, 무차별 대입 방법입니다.

이중 중첩 반복문을 통해 배열 내 두 숫자 nums[x], nums[y]를 선택하여 더한 후 target과 동일한지 확인합니다.

만약 target과 동일하다면 두 수의 인덱스 x, y를 반환하며, 답이 없다면 빈 배열을 반환합니다.

for (int x = 0 ; x < nums.size() ; x++) {
    for (int y = x + 1 ; y < nums.size() ; y++) {
        int sumResult = nums[x] + nums[y];
 
        if (target == sumResult) {
            return std::vector<int>{x, y};
        }
    }
 
    return std::vector<int>();
}

정말 간단하게 배열 내 모든 원소를 순회하면서 nums[x]와 nums[y]를 선택합니다.

두 값의 덧셈을 sumResult 변수에 임시로 저장 후 target과 비교하여 정답인지 아닌지 찾습니다.

다만 특별한 점이라면 내부의 중첩된 반복문은 x + 1번째부터 시작합니다. 이러한 이유는 문제의 제약조건인 같은 수를 두 번 이상 사용하지 않기 위해서입니다.

만약 x == y == 0라면 nums[0] + nums[0]이므로 제약조건에 위배됩니다.

두 번째로 2 + 4 == 4 + 2의 경우도 제거하기 위해서입니다.

x = 1, y = 4인경우 nums[1] + nums[4]는 x = 4, y = 1일경우 nums[4] + nums[1]과 동일하기에 불필요한 탐색입니다.

Solution 1 - 제출 결과

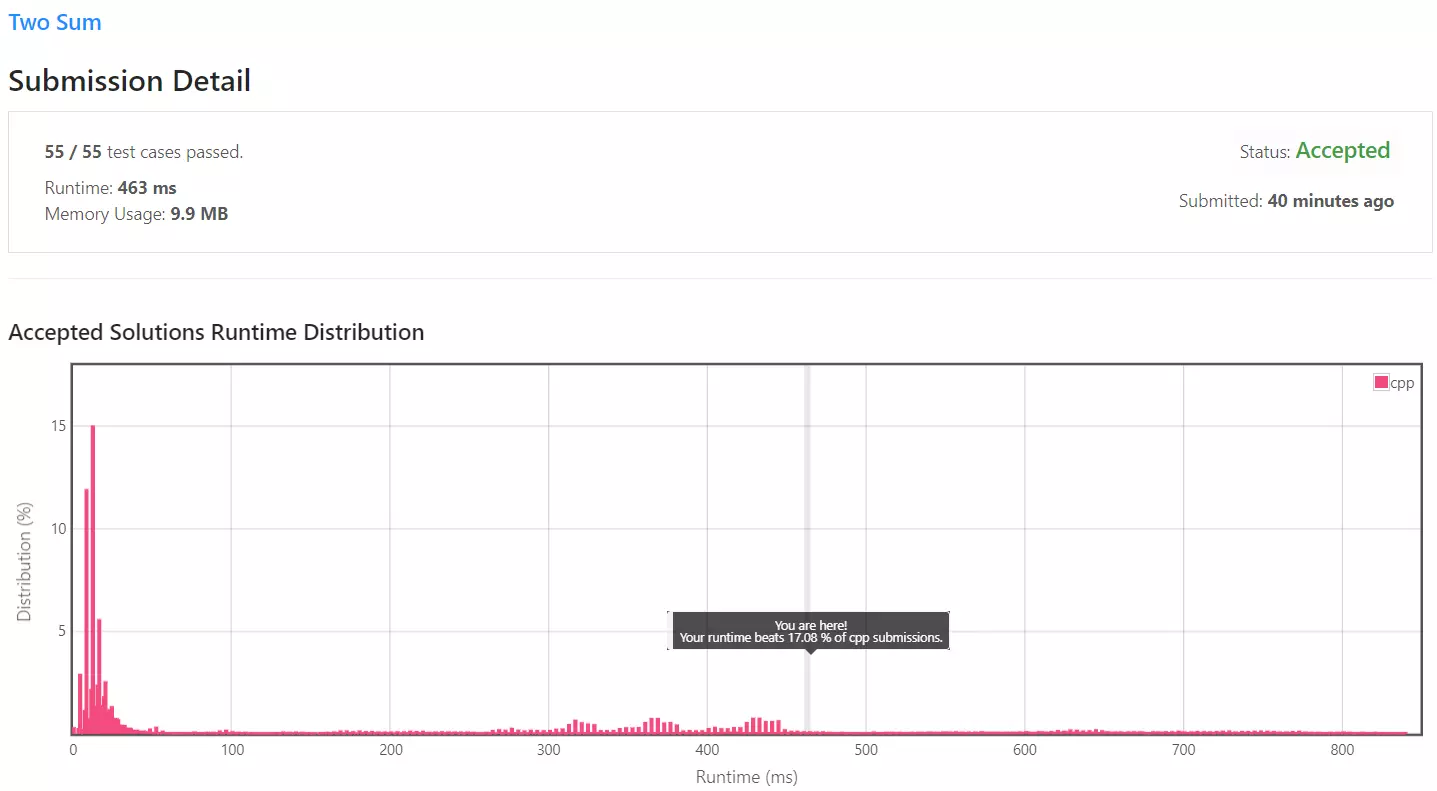
Solution 1 result

실행 시간은 463ms 소요되었으며, 메모리는 9.9MB 사용되었습니다. 실행 시간 기준 하위 17% 정도에 위치하고 있습니다.

이중 중첩 반복문을 사용하고 있기에 $O(n^2)$ 의 실행 시간을 갖는 알고리즘입니다.

코드 전문

#include <vector>
 
class Solution
{
public:
    std::vector<int> Answer(std::vector<int>& nums, int target)
    {
        for (int x = 0 ; x < nums.size() ; x++)
        {
            for (int y = x + 1 ; y < nums.size() ; y++)
            {
                int sumResult = nums[x] + nums[y];
 
                if (target == sumResult)
                {
                    return std::vector<int>{x, y};
                }
            }
        }
 
        return std::vector<int>();
    }
};

Solution 2 - Hash table

첫 번째 방법은 $O(n^2)$ 의 실행 시간을 갖는 알고리즘입니다. 따라서 이보다 빠른 알고리즘을 찾을 필요가 있습니다.

첫 번째 방법이 $O(n^2)$ 의 실행 시간을 갖는 이유는 배열을 중첩 반복문에 배열을 n*n번 순회하기 때문입니다. 이러한 이유는nums[0 ~ n] + nums[0 ~ n]까지 모든 가능성을 테스트하기 때문에 n*n번의 순회가 필요하게 됩니다.

우린 이러한 탐색 과정을 최적화할 필요성이 있습니다.

현재 숫자를 찾을 때 nums[x] + nums[y] = target인 경우를 계속 탐색하고 있습니다. 이 연산을 조금 바꾸면 target - nums[y] = nums[x]가 됩니다.

그러므로 여기서 배열 내에 target- nums[y]에 대하여 nums[x] 값이 존재한다면 인덱스 (x, y)가 답이 될 것입니다.

만약 nums[x]가 배열 내에 없다면? target - nums[y + 1], target - nums[y + 2]... 인 경우에 대해서 탐색해야할 것 같습니다.

결국 똑같이 모든 경우를 탐색해야 하니 $O(n^2)$ 의 방법을 가지게 될까요?

이를 해결하기 위해 Hash Table이라는 저장 공간을 사용합니다. Hash Table은 Key:Value 형태의 자료구조입니다.

Map, Dictionary같은 자료구조와 비슷하지만, Hash 함수를 이용해 인덱스를 생성하므로 삽입과 탐색이 $O(1)$ 로 정의되기에 탐색에서 큰 장점을 보이게 됩니다.

C++에서 Hash Table은 STL unordered_map container으로 제공되고 있습니다.

배열을 순회하면서 현재 원소의 값을 Key로 인덱스를 Value로 사용하여 Hash Table에 저장합니다.

//                num, index
std::unordered_map<int, int> table;
...
table.insert(std::make_pair(nums[x], x));

각 원소에 대해 diff = target - nums[x], target과의 차를 계산한 후 diff를 Key로 Hash Table에서 찾습니다.

int diff = target - nums[x];
 
auto search = table.find(diff);
if (search != table.end()) {
    return std::vector<int>{x, search->second};
}

만약 Table내에 diff에 대한 Key가 존재한다면 배열 내에 diff와 똑같은 값을 가지는 원소가 존재한다는 의미입니다.

아까 Hash Table에 저장할 때 원소의 값을 Key, 인덱스를 Value에 저장했으므로 현재 반복문의 인덱스와 Hash Table에 저장된 인덱스를 반환하면 됩니다.

Hash Table의 삽입/탐색 속도는 $O(1)$ 이고, 단일 반복문으로 배열을 n번 순회하므로 본 알고리즘은 $O(n)$ 의 실행 시간을 가지게 됩니다.

Solution 2 - 제출 결과

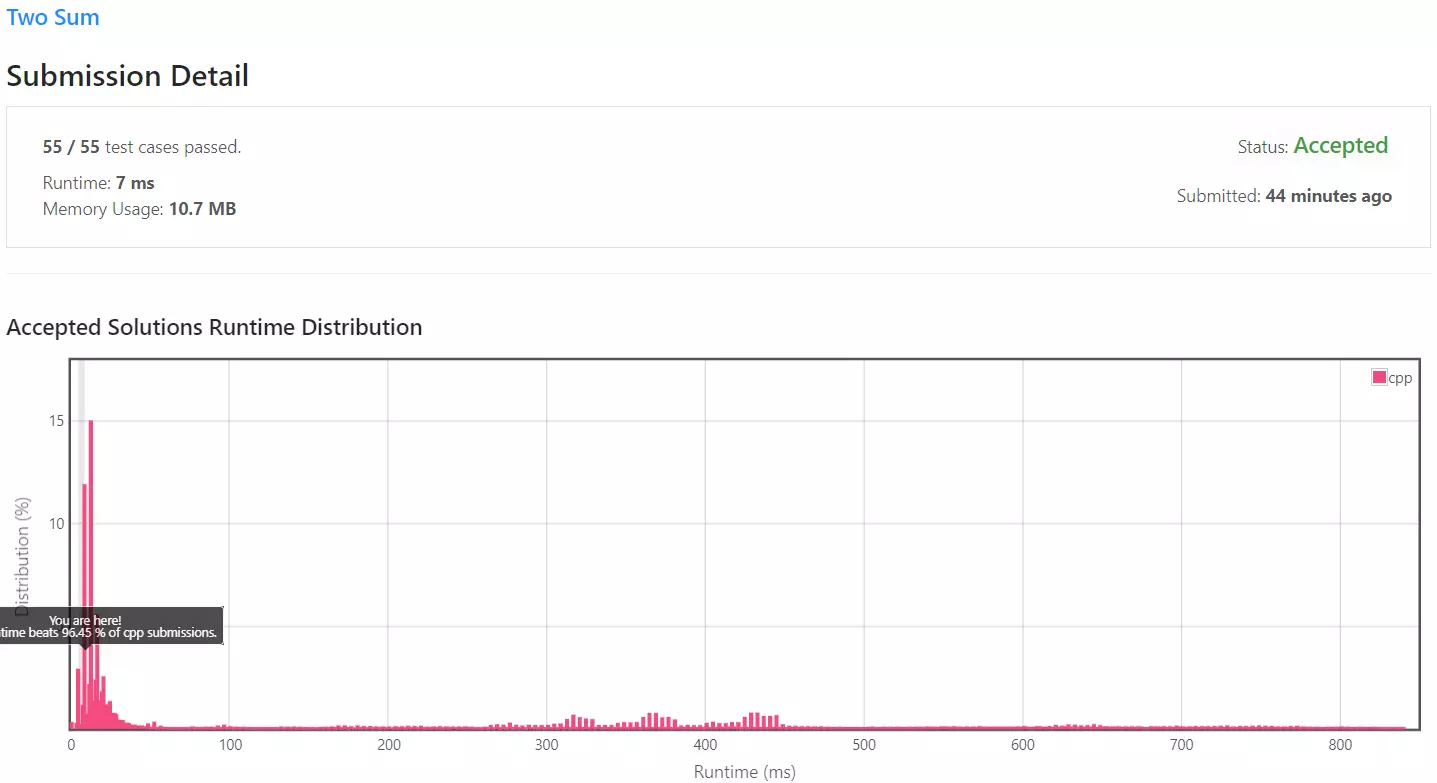
Solution 2 result

기존의 약 500ms의 속도에서 7ms의 속도로 70배 가까이 향상되었습니다.

다만 별도의 저장 공간을 사용했기에 메모리의 크기가 9.9MB에서 10.7MB로 증가했습니다.